[계량경제학] panel data

Minwu Kim
2024년 4월 10일
2분 분량

링크(누군지는 모르겠으나 너무 야무지게 정리를 잘 해주심. 때땡큐입니다)

1.Panel data란

Panel data를 이해하기 위해선 cross-sectional data와 time series data를 이해해야 한다.

Cross-sectional data란 하나의 시점에 여러가지 개체의 데이터를 수집한 것이다.

Time series data란 여러가지 시점에 하나의 개체의 데이터를 수집한 것이다.

Panel data는 여러가지 시점에 여러가지 개체의 데이터를 수집한 것이다. Cross-sectional data와 time-series data의 특성을 모두 갖춘 데이터이다.

2. Pooled OLS

Panel data로 선형회귀를 할 수 있는 아주 단순 무식한 방법은 바로 개체와 시간에 대한 요인을 고려하지 않고 그냥 cross-sectional data로 취급하는 것이다.

수식은 아래와 같다. i는 객체를, t는 시간을 의미한다.

OLS estimator가 consistent 하려면 exogeneity를 만족해야 한다. 수식은 아래와 같다.

또한 OLS estimator 효율적이려면 autocorrelation이 없어야 하며, 시계열적 상관이 존재하지 않고 등분산성을 충족해야 한다.

3. Unobserved heterogeneity

하지만 panel data를 cross-sectional data 취급하면 생기는 문제가 있다. 바로 객체 고유의 오차를 고려하지 않는다는 것이다. 예를 들어, 성적과 공부시간으로 regress한다고 해보자. 수식은 아래와 같다.

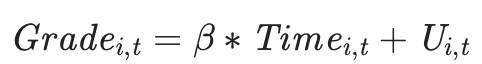
이 식의 오차항에는 공부시간 외의 관측되지 않은 다른 요인들이 포함되어 있다. 이를테면 학생의 컨디션, 가정환경, 학원비용 등등이 있다.

그 중에는 시간과는 무관한 부분도 있다. 예를 들어 공부습관이 잘 단련 된 학생이나, 지능이 높은 학생들은 성적이 좋을 확률이 높다. 이런 경우 공부시간이 동일하더라도 습관 좋고 지능 높은 학생들은 그렇지 않은 학생보다 오차항의 크기가 더 클 것이다.

이런 객체 고유의 오차, 즉 시간과는 상관없는 오차를 unobserved heterogeneity라고 한다.

Pooled OLS의 단점이 바로 이 unobserved hetereogeneity를 반영하지 못한다는 것이다. 모든 data instance를 독립적으로 취급하기에 학생들 고유의 오차를 잡아낼 수가 없다.

고로, 우리는 이와 같이 모델링을 오차항을 두 부분으로 나눌 수 있다:

individual(unit) effect: time-invariant한, 즉 객체 고유의 오차이다. 앞서 얘기한 학생의 기본 지능이나 공부습관 등이 있다.
idiosyncratic error: time-variant한 오차이다. 선생님의 퀄리티, 학원가의 퀄리티 등이 있겠다.

수식은 아래와 같다:

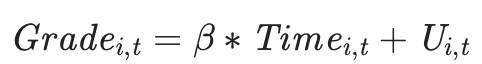
idiosyncratic error는 일반적인 cross-sectional data의 OLS와 통계적 특성이 동일하다:

4. Random Effect Model

앞선 내용을 정리하자면 아래와 같다:

그리고 이 estimator가 consistent하려면 아래와 같은 조건이 충족되어야 하는데

이 조건은 또 아래와 같이 쪼갤 수 있다:

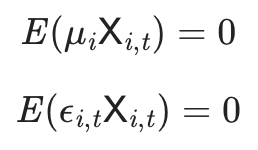
첫줄을 보이듯, random effect 모델에선 individual effect 역시 X에 대해 exogeneity를 갖는다. 참고로 이것이 0이 아닌 경우 해당 pooled OLS는 "heterogeneity bias"가 있다고 묘사한다.

문제: autocorrelation -> 하지만 exogeneity가 만족이 되었더라도 Pooled OLS는 더 이상 BLUE하지 않다. autocorrelation 때문이다:

이를 해결하기 위해 통상적으로 두가지 방법이 있다.

kerneling(몰라도 됨)
between estimator

일단 커널링은 아래와 같다:

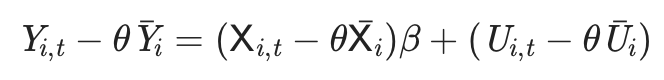
heteroskedaticity-robust한 OLS가 다 이런 식인데, 아직 이게 뭔지는 잘 모르겠다. 나중에 시간 나면 봐봐야겠다.

그 다음이 BE (between estimator)이다. 객체 마다의 평균치로 회귀를 하는 것이다. 하지만 이건 데이터를 너무 많이 날려먹는 단점이 있다.

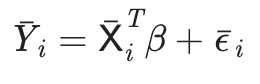
5. Fixed Effect Model

Fixed effect model에서 random effect model과 달리 individual effect가 독립변수와 상관된다. 고로 POLS 방법으로 일관된 추정량을 구할 수 없다. 수식으로 표현하면 이런 식이다 (저기 부등식 주의)

이 individual effect를 제거해야만 POLS가 consistency를 유지할 수 있다:

일단 할 수 있는 것은 First Differencing (FD) 이다.

두개의 consecutive한 시간의 차이를 구하는 것이다. 그렇게 individual effect를 소거한다.

또 가능한 것은 Between Equation(BE), 혹은 Fixed Effects(FE), 내지는 within estimator이다. 평균을 구하고 빼주는 식이다.

하지만 이 두가지 방법론의 문제는 individual effect를 그대로 소거해버린다는 것이다. 그래서 쓸 수 있는 것이 Least Square Dummy Variable, LSDV이다. 즉, 각 객체마다 individual effect를 dummy variable의 형태로 가져가는 것이다.

LSDV 방법에서는 고정효과가 관측된 독립변수로 포섭되었기 때문에, exogeneity를 고려해야 할 오차는 고유오차뿐이다. 그리고 고유오차는 모형의 독립변수들과 모두 직교하므로 OLS 방법이 일치 추정량을 제공한다. 또한 개체마다 다른 개별효과까지 추정한다.

Minwu Kim

댓글